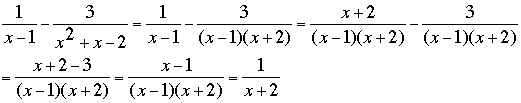Hi Jonathon,

These are not polynomials they are rational functions. A rational function is a function that can be written as a polynomial divided by a polynomial. You add rational functions just as you would add rational numbers (fractions) by first finding a common denominator. For example to add 1/3 and 1/15 I can see that 15 = 3 × 5 so 15 is a common denominator and hence

Now let's try 1/(x - 1) - 1/(x² + x - 2). Again I need a common denominator and since x² + x - 2 = (x - 1)(x + 2) I can use x² - x - 2 as a common denominator. Thus

Now you try 1/(x+3) + 1/(x^2+5x+6) .

If you need further assistance write back.
Penny