| |||
| Math Central | Quandaries & Queries |
|
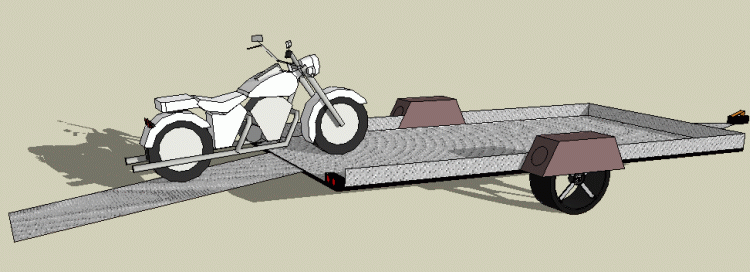
Question from Joshua, a parent: I am currently building a motorcycle trailer. I am trying to figure out the length of the ramp so that the bikes don't scrap the trailer/ramp as they are loaded. This is the info I have: the motorcycle is 6" off the ground in the center, the point where the tires touch the ground are 80" apart, the trailer deck is 20" high. How do I figure the length of the ramp? Please show equation so I have for future reference with different measurements. |
Hi Joshua.
I am picturing something like this:
For which we can label the relevant geometry as shown below (not to scale!)
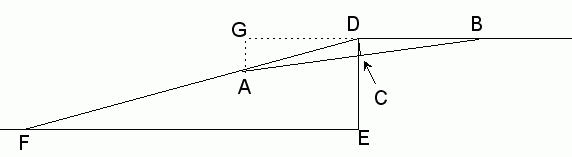
We know:
DE = 20 inches
DC < 6 inches
AB = 80 inches
We'll use DC = 6 inches to find the minimum length for DF.
Note that we are inferring that the closest the bike chassis comes to grounding is where the wheels are an equal distance from the end of the trailer.
Thus, AC = BC, so BC = 40 inches.
Since triangles GAD and EDF are similar, the ratios of corresponding sides are the equal. So FD / DE = DA / AG.
Thus,
FD = DE ( DA / AG)
Now in the triangle GAB, AG = AB sin B. From triangle BDC we can see that sin B = DC/BD so we have:
FD = DE ( DA × BD) / ( AB × DC)
But DA = BD so FD = DE × DA2 / ( AB × DC)
and using the pythagorean theorem, DA2 = AC2 + DC2.
So now we have:
FD = DE × (AC2 + DC2) / ( AB × DC)
And we know all the values on the right side of the equation, so we can substitute them in. The equation above could be used for any clearance, wheel base and bed height.
Without the variables we could write it this way:
Minimum ramp length =
BedHeight x ( (Wheelbase / 2)2 + Clearance2 ) / ( Wheelbase x Clearance )
Let's use the values you provided:
FD = 20( 402 + 62 ) / ( 80 × 6 )
which my calculator says is 68.2" inches.
I'll leave it to you to draw it to scale on graph paper to verify that's a reasonable answer.
Cheers,
Stephen La Rocque and Harley Weston.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.