Hi Jyotishman,

This problem involves geometry and calculus. The geometry tells me what it is I need to find and the calculus gives me a method to find it. I can get you started.

First I graphed y = f(x) = x³ - 13x + a with a = 0. The axes are in red and I didn't put the scale on the axes since I am interested in the shape not the scale. This graph crosses the x-axis in 3 places marked by the red dots.

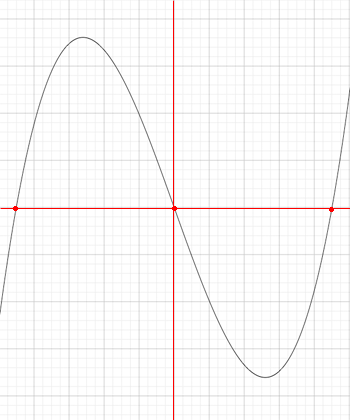
As a increases he graph moves upwards relative to the axes maintaining three distinct zeros until

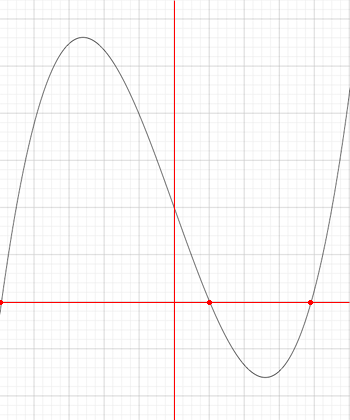
until a attains a value for which the polynomial f(x) = x³ - 13x + a two distinct roots, one of them I am going to call p as in the diagram. (One root is not on my diagram.) O

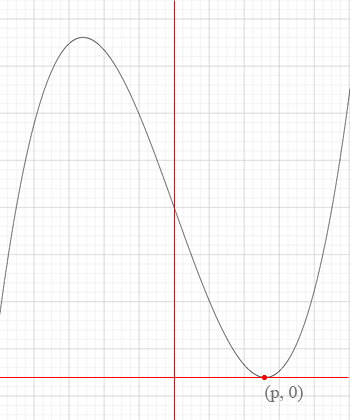
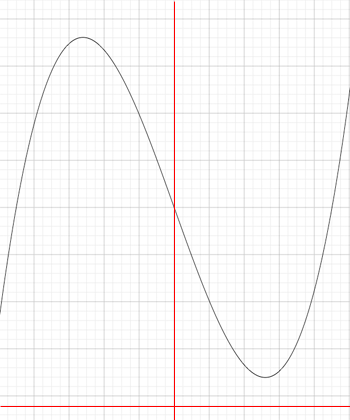
If a increases beyond this value the resulting graph only crosses the x-axis at one point (not on the diagram).

The task is thus to find p and then the value of a so that f(p) = p³ - 13p + a = 0.

p is a critical value for the polynomial f(x) so it can be found by solving f '(x) = 0.

Do you now see how to complete the problem? If you need further assistance write back.

Harley