Hi Karan,

I can show you a way to count them yourself and help you discover an expression that will work for any convex polygon.

Draw a The diagonals of a hendecagon, choose a vertex and call it P and the draw every diagonal from P to another vertex.

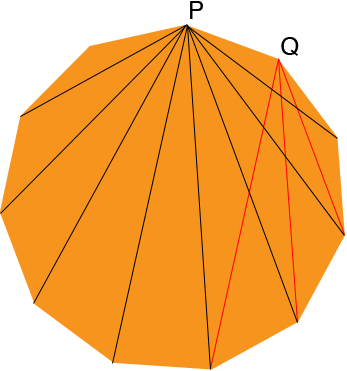
Count the number of diagonals you drew. I got 8. Why 8?

Move to an adjacent vertex, I called it Q. Draw all the diagonals through Q being careful not to draw a diagonal if if you already drew it before. I just drew a few. How many did you get?

Move to an adjacent vertex. Draw all the diagonals through this vertex being careful not to draw a diagonal if if you already drew it before. How many did you get?

Continue around the hendecagon drawing the diagonals from each successive vertex being careful not to draw a diagonal if if you already drew it before.

Write down the sequence on numbers you obtained. The sum of this sequence is the number of diagonals of a hendecagon. Do you see the pattern in the sequence of numbers? How many diagonals does a regular polygon with 15 sides have?

Penny