| |||
| Math Central | Quandaries & Queries |
|
Question from Kate, a student: I am working on the Law of Sines and I have a problem that says: Find a value for b so that the triangle has 2 solutions. I am given that A = 36 degrees and a = 5. Now, I learned that for a triangle to have 2 solutions, h < a < b. BUT...my answer key says the answer is: 5 < b < 5/sin 36. I can't figure out how to make this fit with h < a < b. Please help if you can! Thanks! |
Hi Kate,
Look at my diagram
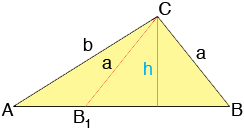
The lengths a and b are given as is the measure of the angle at A. There are two possible configurations, triangle ABC and AB1C. In fact the measure of the angle B1 is 180o minus the measure of the angle B.
From the diagram sin(B) = h/a and hence sin(B)/b = h/(ab). But by the law of sines sin(B)/b = sin(A)/a and hence
sin(A)/a = h/(ab)
and thus
sin(A) = h/b or h = b sin(A)
Thus if h < a then b sin(A) < a. You have A as 36 degrees and sin(36) is positive so b < a/sin(A) = 5/sin(36).
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.