Hi Katie,

I am going to answer your question but for the expression x³ - 2x².

I think about this question in terms of the graph of the expression y = x³ - 2x². I want to know when the graph lies above the x-axis (that is when x³ - 2x² > 0), when it is below the x-axis (that is when x³ - 2x² < 0) and when it intersects the x-axis (that is when x³ - 2x² = 0).

To determine when x³ - 2x² = 0 I factor x³ - 2x² to obtain x³ - 2x² = x²(x - 2) and hence x³ - 2x² = x²(x - 2) = 0 when x = 0 and when x = 2. These two x-values divide the x-axis into three pieces

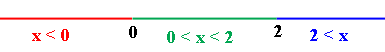
I now choose an x-value in the leftmost piece, x < 0. I want an x-value that is easy to calculate with so I choose x = -1. At x = -1, y = x³ - 2x² = (-1)³ - 2(-1)² = -1 -2 = -3. Thus the graph of y = x³ - 2x² is below the x-axis at x = -1. The important point here is that the graph is thus below the x-axis for all x satisfying x < 0 since to go above the x-axis the graph would need to cross the x-axis and it doesn't touch the x-axis until x = 0.

Now choose a point in the next piece of the axis, 0 < x < 2. Again I want an easy point so take x = 1. At x = 1, y = x³ - 2x² = 1³ - 2(1)² = 1 -2 = -1. Thus the graph of y = x³ - 2x² is below the x-axis at x = 1 and thus below the x-axis for all x in 0 < x < 2 since it doesn't touch the x-axis again until x = 2.

Finally choos a point in the remaining piece of the x-axis, 2 < x. This time I take x = 3 and at x = 3, y = x³ - 2x² = 3³ - 2(3)² = 27 - 18 = 9 and the graph is above the x-axis at x = 3 and therefore above the x-axis fo all x satisfying 2 < x.

Thus my answer is x³ - 2x² ≥ 0 for 2 ≤ x and for x = 0.

Just as a check here is the graph of y = x³ - 2x².

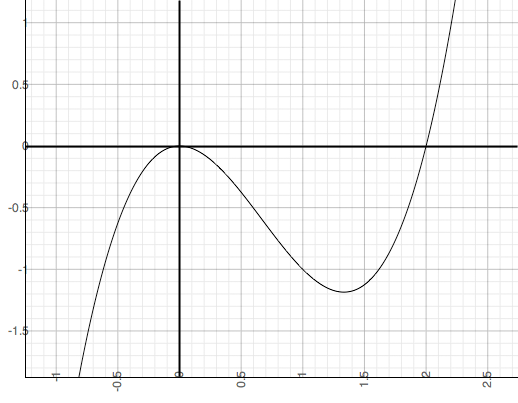
Penny