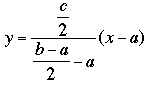The intersection of the medians

HOME

Math Central

Quandaries & Queries

Question from Katie, a student:

Q: A Triangle is positioned with one side on the x-axis, the coordinates
for the triangle are (-a,0), (a,0), (b,c)

a) Find the coordinates of the point of intersection of the perpendicular bisectors of the sides
b) Find the coordinates of the point of intersection of the medians
c) Find the coordinates of the point of intersection of the altitudes

I've spent nearly hours trying to figure out these questions, and i can't seem to get anywhere, please help me, if not with all of them, then with letter b, if at all possible... Thx

Hi Katie,

Let's look at b). A median of a triangle joins a vertex to the midpoint of the opposite side.

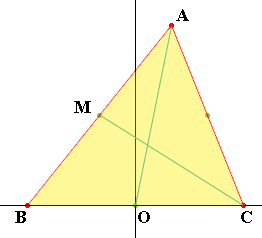
triangle

In my diagram B has coordinates (-a,0), C has coordinates (a, 0) and A has coordinates (b,c). O is the origin which is the midpoint of BC and M is the midpoint of AB. M has coordinates ((b - a)/2, c/2).

The median from A to O has equation

y = c/b x

and the median from C to M has equation

which simplifies to

To find the coordinates of the intersection of the medians AO and CM solve the two equations. Setting the y-coordinates equal gives the equation

Solving for x I found x = b/3. Then I substituted x = b/3 into the equation for the median AO and found y = c/3. Thus the medians intersect at (b/3, c/3).

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.