| |||
| Math Central | Quandaries & Queries |
|
Question from kobina, a student: You are traveling on an airplane that is moving at 500 mph in a direction 40deg north of west.Therefore , You are travelling (due to the plane ) at how many mph towrd the west. |
Hi Kobina.
Let's draw a right angled triangle showing the north-south direction and the east-west direction.
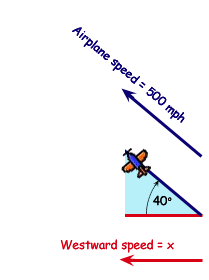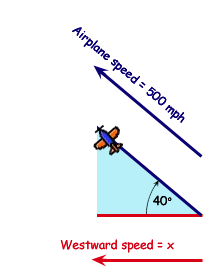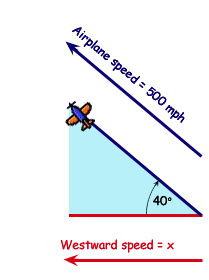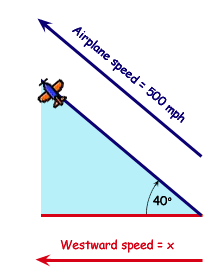
As you can see, the lengths of the lines indicate the speeds. Can you see how the length of the bottom line represents the speed the airplane travels westward?
How long that line is depends on the angle and the length of the hypotenuse. We can use the Cosine function (COS) to find the length of a leg of a right-angled triangle when we know the length of the hypotenuse and the angle between them.
Cosine = adjacent / hypotenuse
So in your case, the hypotenuse length is the speed of the actual airplane (500mph) and the angle is 40 degrees. Let's let the length of the unknown east-west line be x mph. We have:
|
cos( 40o ) = x / 500 x = 500 cos( 40o ) x = 383 mph. |
The answer is 383 mph. We call this the component of the speed of the airplane that is moving westwards.
Hope this helps,
Stephen La Rocque
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.