| |||
| Math Central | Quandaries & Queries |
|
Question from Kristina, a student: A square with side lengths of 6 cm is divided into 3 right triangles and a larger isosceles triangle. If the three right triangles have equal area, find the exact area of the isosceles triangle. |
Kristina,
Try this shape.

Stephen La Rocque.
If you need more help, scroll down.
Determine the three variable relationships:
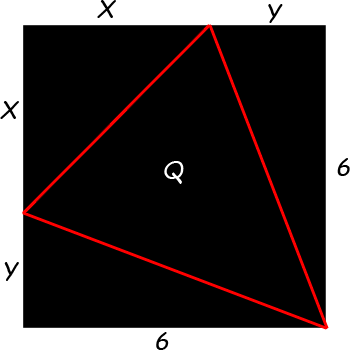
This diagram labels the lengths that we need to consider as well as the area Q of the large isosceles triangle. We have three variables, so we need three distinct equations to solve the problem. They are:
(1) Side length: x + y = 6
(2) Equal areas: ½x2 = 3y
(3) Total area: ½x2 + 3y + 3y + Q = 62.
Scroll down if you still need more hints.
Get rid of y:
Combine the first two equations using the substitution method:
| ½x2 = 3y | x + y = 6 | |
| x2 - 6y = 0 | y = 6 - x | |
| x2 - 6(6 - x) = 0 x2 + 6x - 36 = 0 |
||
Now use the Quadratic Formula to solve for x. Since x is a length, we can ignore the negative solution and choose just the positive solution.
Scroll down for more of the solution.
Quadratic formula:
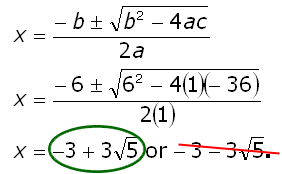
Next, we can combine equations (1) and (3) to solve for Q, the area we have been asked to find:
| ½x2 + 3y + 3y + Q = 62 | x+y=6 | |
| Q = 36 - ½x2 - 6y | y=6-x | |
| Q = 36 - ½x2 - 6(6-x) Q = 6x - ½x2 |
||
And finally, substitute the value for x that we calculated earlier into this expression.
Final calculation:
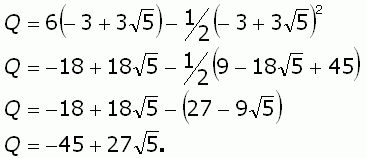
Solved. You can check by calculating y and the area of each triangle and seeing that they add to 36 square centimeters.
Stephen.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.