Hi Lewis,

I assume you mean a regular octagon where all the sides have the same length and all the angles have the same measure.

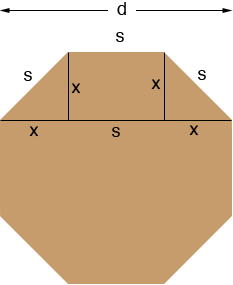
In my diagram the diameter is d and the side length is s. From the diagram you can see that

d = s + 2x

Since you know that s = 60 feet all that remains is to find x. This we can do using Pythagoras Theorem. The small triangles with sides of length x, x and s are right triangles so, using Pythagoras Theorem,

s² = x² + x² = 2x²

so

x = s/√2

Thus

d = s + 2x = d = s + 2(s/√2) = s + √2 s = (1 + √2) s

In your case s = 60 feet so

d = (1 + √2) × 60 = 144.85 feet.

Penny