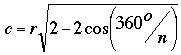Hi Lindsay.

Here's a method that solves this problem for any regular n-gon inscribed in a circle of radius r.

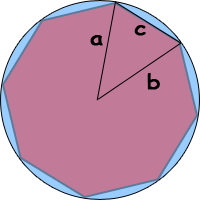A regular n-gon divides the circle into n pieces, so the central angle of the triangle I've drawn is a full circle divided by n: 360°/n.

The Law of Cosines applies to any triangle and relates the three side lengths and a single angle, just as we have here. In general it says this:

In the case of our regular n-gon, we have a = b = r and C = 360°/n, so we simplify it to:

c² = r² + r² - 2rr cos (360°/n)
c² = 2r² - 2r² cos (360°/n)
c² = r² (2 - 2 cos (360°/n))

which makes a final equation:

If you wanted the perimeter of the n-gon, you would just multiply this by n of course.

For your question Lindsay, just put 5 units in for r and 8 in for n and you can calculate c.

Hope this helps,
Stephen La Rocque