| |||
| Math Central | Quandaries & Queries |
|
Question from Linnea, a student: I have a tringle with a circle inscribed in it. My teacher wants me to find the radius of the circle. This is what she gave me to work with. The triangle is ABC, AB = AC = 6, and BC = 4. She also told us to use A(squared) + B(squared) = C(squared). and that there are altitudes and and incenter. I have no idea how to do this. |
Hi Linnea,
I drew the triangle and circle and lines form the centre of the circle to the points where the sides of the triangle are tangent to the circle, that is the points Q, R and S.
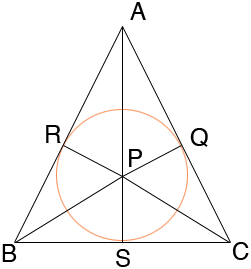
Since Q, R and S are points of tangency the three radii meet the triangle sides in right angles. From this you can see that triangles PSC and QPC are congruent, triangles PQA and ARP are congruent and triangles PRB and PBS are congruent. Since |CA| = |AB| you can also conclude that triangles PBS and PSC are congruent and therefore |BS| = |SC| = 2. By observing the congruent triangles you can also conclude that APS is a straight line and hence triangle ASC is a right triangle.
Apply Pythagoras Theorem to triangles PSC anf ASC.
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.