Hi Lisa,

In my triangle ADC the lengths of AD and CA are each equal to 8.4 cm. The area of the triangle ADC is

25.6 = 1/2 b h

where b is the length of the base DC and h is the height, AC.

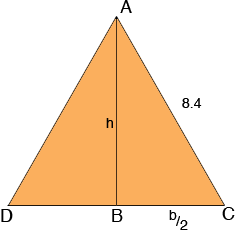
Triangle ABC is a right triangle and hence by Pythagoras' Theorem

h² + (b/2)² = 8.4² or b/2 = √[8.4² - h²]

Substitute this value for b/2 into the expression for the area to get

25.6 = h √[8.4² - h²]

At this point I would square each side to eliminate the square root. This gives a quartic in h but if you substitute x = h² then you have a quadratic in x which you can solve. Finally h is the square root of x but remember that h must be positive.

Penny