| |||
| Math Central | Quandaries & Queries |
|
Question from Liz: A rectangular pool 50ft long and 30ft. wide has a depth of 8 ft. for the first 20 ft. for its length and a depth of 3 ft. on the last 20ft. of its length and tapers linearly for the 10 ft in the middle of its length. the pool is being filled with water at the rate of 3ftcubed/ min |
Hi Liz,
Here is my sketch of the pool with water water at a height of h feet.
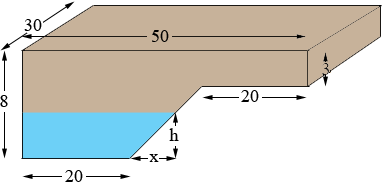
The fraction h/x is the slope of the tapered edge which is 5/10 = 1/2. Thus h/x = 1/2 and thus x = 2h.
The volume of water in the pool at height h, V(h), is the area of the blue trapezoid times the width of 30 feet. The area of a trapezoid is the average of the length of the parallel sides times the distance between the parallel sides. Thus
V(h) = (20 + x + 20)/2 × h × 30
= (40 + 2h)/2 × h × 30
= 30 × (20 + h) × h
Try to complete the problem from here. If you need further assistance write back.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.