We have two responses for you

Hi Lucy,

That's a very nice observation. If you have a three sided polygon (a triangle) and you know the side lengths then the figure is rigid and it should be possible to find the angles. If you have a polygon with more than three sides and you know the side lengths then the figure is not rigid and the angles can vary.

The relationship you are looking for is called the Law of Cosines. I can show you a proof at least for an acute triangle. If the triangle isn't acute you have to modify my proof slightly.

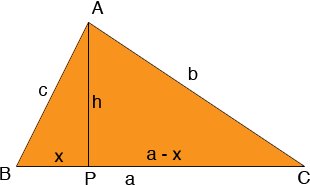
The triangle ABC has side lengths a, b and c. Draw AP perpendicular to BC, let h be the length of AP and x be the length of BP, then the length of PC is a - x.

Write Pythagoras' theorem for the two right triangles

x² + h² = c²
h² + (a - x)² = b²

I need one further equation

cos(C) = (a - x)/b or
a - x = b cos(C)
and thus
x = a - b cos(C)

Expand the second equation to get

h² + a² - 2ax + x² = b²

Using the first equation replace x² + h² by c² then using the third equation replace x by a - b cos(C). Simplify to get

c² = a² + b² - 2ab cos(C)

This is the Law of Cosines. If you know the side lengths a, b and c you can find cos(C) and hence the measure of the angle C.

Harley

Hi Lucy.

Here's an example of how I would use Harley's "Law of Cosines" to find the angles of a triangle.

Let's say I am told the sides lengths are 10, 4 and 7.

First I should assign reference letters.
Let side a = 10, side b = 4 and side c = 7.

By convention, the angles (or corners) of the triangle are capital letters corresponding to the side that is across from them. So I have this diagram, labelled appropriately:

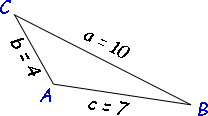
Start by picking an angle to use the law of cosines for. I'll choose angle C:

c² = a² + b² - 2ab cos(C)
7² = 10² + 4² - 2(10)(4) cos(C)
-67 = -80 cos(C)
cos(C) = 0.8375

To solve for C, we have to "undo" the cos() on the left hand side. We do this using arccos or cos^-1 (which mean the same thing: inverse cosine). But then we must do this to both sides of the equation:
cos^-1 (cos(C)) = cos^-1 ( 0.8375 )
C = cos^-1 (0.8375)

**When you use a calculator for trigonometric functions, you really have to pay attention to whether you are in degrees or radians (or gradians). This is usually indicated on the calculator as D or R or G and there might be a button called DRG that lets you change to that mode. Be sure you are using Degrees unless you know you want Radians (gradians are rarely ever used in mathematics).

So in Degrees mode, my calculator solves this as C = 33.12 degrees.

Now I'll pick another angle in the triangle: angle B. First I rewrite the law of cosines in terms of angle B:

b² = a² + c² - 2ac cos(B)

You can rewrite the law of cosines in terms of any angle, you just have to make sure that the angle you want is inside the Cos ( ) and the side opposite it is on the other side of the equal sign.

Now let's solve it the same way:

4² = 10² + 7² - 2(10)(7) cos(B)
-133 = -140 cos(B)
cos(B) = 0.95
B = cos^-1 (0.95)
B = 18.19 degrees

The last angle is simpler. Since all triangles have the property that the sum of the angles is 180, we just subtract:

A = 180 - 33.12 - 18.19 = 128.69 degrees.

So that's how it is solved.

Hope this example helps,
Steve La Rocque.