Manashi,

To answer your second question you can multiply matrices of the same dimensions by multiplying corresponding elements. It's called the Hadamard Product. The Hadamard Product has many nice properties, in particular if A and B are both m by n matrices then A*B = B*A if * is the Hadamard Product. For the usual matrix product even if A and B are square matrices so that you can find AB and BA it may not be true that AB = BA. As to your first question division is still a problem if multiplication is the Hadamard Product. If you divide matrices of the same dimension by dividing corresponding elements the A divided by B will not exist if the matrix B has any zero entries. The Hadamard Product is studied by mathematicians interested in matrix theory and current research is being done in this area.

Why then do we learn this other, somewhat bazaar looking multiplication called matrix multiplication. The answer is that it is extremely useful. The operation comes from seeing a matrix as a linear transformation.

Suppose A is a 2 by 2 matrix then 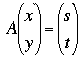. That is A times a 2 by 1 matrix is a 2 by 1 matrix. If and are points in the plane (more conventionally written (x,y) and (s,t)) then A can be seen as a function from the plane to the plane called a linear transformation. If B is also a 2 by 2 matrix then B is also a linear transformation. So what if you transform by A to get and then you transform by B? What do you get? That is what is 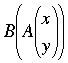? It is the result of result of transforming by the matrix BA, the matrix product of B and A. What I am saying is that if you view matrices as linear transformations then matrix multiplication is the composition of the functions.

I hope this helps,
Harley