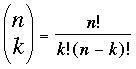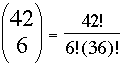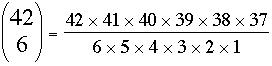 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Marcus: If i have 42 numbers to choose from and i could only choose 6 numbers at a time without choosing the same number twice in the same row, how many possibilities are there? |
Hi Marcus,
The number of ways of choosing 6 objects from 42 objects is called 42 choose 6 and is written by mathematicians as 
but sometimes you see it designated 42C6. The definition is
where k! = k × (k-1) × (k-2) × (k-3) × ··· × 1. (For example 5! = 5 × 4 × 3 × 2 × 1 = 120.) Thus
After some simplification this becomes
I'll let you do the arithmetic.
Penny
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.