Mark,

In my diagram r is the radius of the circle, c is half the chord length and h is height of the arc above the chord.

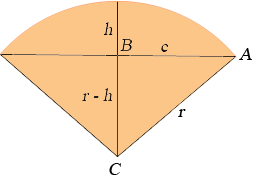
Triangle ABC is a right triangle and hence, by Pythagoras' theorem

r² = (r - h)² + c²
r² = r² - 2rh + h² + c²

and hence

r = (h² + c²)/2h

I changed all your measurements to inches and got

r = (82.75² + 184²)/(2 × 82.75) = 245.943 inches

which is 20' 6".

I didn't need to use the length of the arc so I decided to check my calculations by using a radius of 245.943 inches to calculate the length of the arc. The length a of the arc is given by

a = r θ

where θ is the angle at the centre of the circle measured in radians. The angle BCA is θ/2 and sin(BCA) = c/r. Hence

angle BCA = sin^-1(c/r) = sin^-1(184/245.943) = 0.8453

Thus θ = 2 × 0.8453 = 1.691 radians. Hence

a = r θ = 245.943 × 1.691 = 415.769 inches.

This is 34' 8" which is not the length you have for the arc. Are you sure the arch is an arc of a circle?

Harley