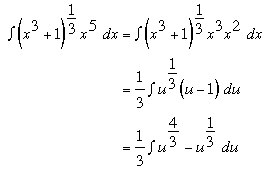Hello Meghan,

The substitution for this integral requires a little trick to eliminate all of the x’s. You have the integral 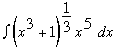  so doing your substitution you let u = x³ + 1 and then du = 3x² dx and simplifying this you get 1/3 du = x² dx. However in our integral we have an x⁵ not an x², but we can split up the x’s in the integral a bit to make it easier for us. So we take our integral and split up the x’s
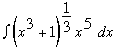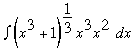=. Now we have an x² from our du statement and we can get an x³ from our u statement. Since u = x³ + 1 then solving for x³ we get x³ = 1 - u now we can substitute. So our process looks like the following.

Then from here you can integrate with respect to u, and then substitute u = x³ + 1 back in after you have integrated to reach your final solution.

I hope this helps. Happy integration.

Brennan Yaremko