We have two responses for you

Hi Michelle,

C is the intersection of the line segments AB and OQ. By the symmetry C is the midpoint of AB and the angles ACO and QCA are right angles.

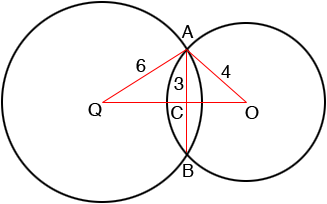
Since triangles AQC and ACO are right triangles you can use Pythagoras' theorem to find the lengths of QC and CO.

Penny

One good way to do this type of problem is to shift your attention.
You start with:

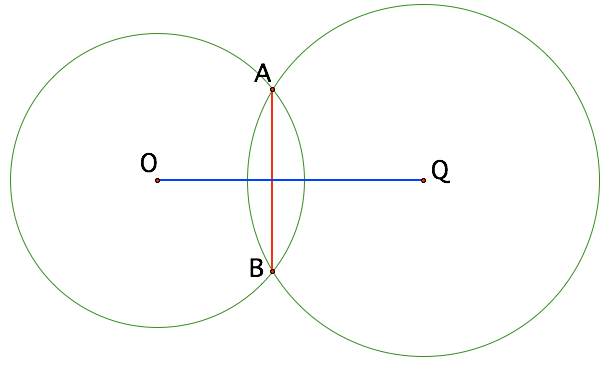
Draw in the radii: OA, OB, QA,QB all of which you know.

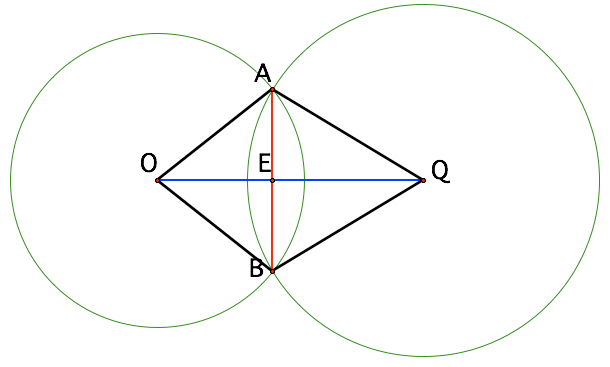
If you drop the circles you can then focus on the two isosceles triangles

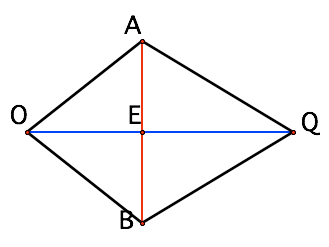
Note that E splits the chord AB so you know AE, EB. OQ is also perpendicular to AB.
You have enough lengths now, and some right angle triangles, so you can compute OE and EQ!

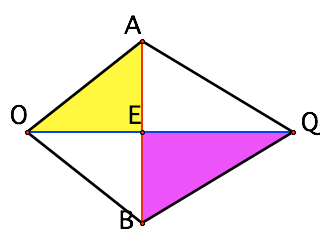
The key is shifting your attention towards the triangles: putting in the known pieces, then extracting the triangles.

Walter Whiteley

Michelle wrote back

Walter:

Thanks for your prompt reply. Regarding this question, the answer is square root of 7 + 3 square root of 3 - which is how long OQ according to the answer in the back of the textbook. My question is how did they come up with that answer?
I used the Pythagoream Theory and I don't come up with that answer. If line OQ is made up of length 4 for Circle O and length 6 for circle Q so instead of 4 and 6 being the one of the legs but more of one base would that help in figuring out this answer? It helps to drop out the circles out of the problem and refocus.
Totally appreciate the quick response. You guys are awesome and your website is helping me with my circle exam on Monday night.

Sincerely,

Michelle

Thanks for the compliment Michelle.

Look at Walter's final diagram. QB is a radius of the circle centered at Q so the length of QB is 6. Since E splits the chord AB the length of EB is 3. Thus you know the lengths of two sides of the right triangle and by using the Pythagorian theorem you can find the length of the third side EQ. In a similar way you can find the length of OE.

Is this what you tried? If you didn't get √7 + 3√3 what did you get?

Penny