We have two responses for you

Hi Michelle,

I agree with your solution but I think there is a typo in the problem. From the statement of the problem

Find two numbers whose sum is 25 and whose product is 120.

I would expect integer solutions. If you change the problem to

Find two numbers whose sum is 26 and whose product is 120.

then your algebraic procedure will produce integer solutions.

With the problem as originally worded I don't se a solution except to use algebra as you did. With my change you have two numbers that satisfy

sum: 26
product: 120

From here you might be able to find the numbers using "Guess and Check". Look for factors of 120 and calculate their sum.

120 = 2 × 60 sum = 62 doesn't work
120 = 3 × 40 sum = 43 doesn't work
120 = 4 × 30 sum = 34 doesn't work
120 = 6 × 20 sum = 26 ok

I hope this helps,
Penny

Hi Michelle,

There are three methods for solving systems of equations: substitution, elimination & graphing. A less accurate way to find the solution would be graphing x+y=25 & xy=120 and find the point where they intersect.

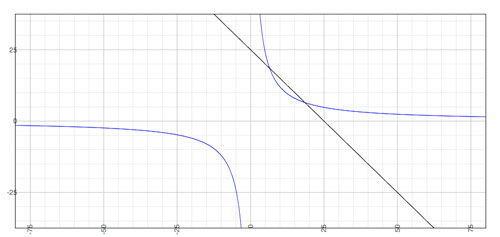
if you have a graphing program it usually has a tool that will find intersections for you.

If the numbers were integers then guess and check would also be an option.

Hope this helps,
Janice