We have two responses for you

Miguel,

It is helpful to have some sample pictures:

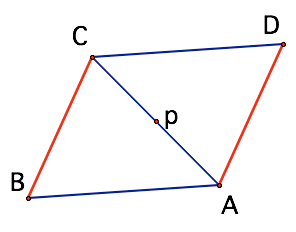
Consider the situation where the two angles <BAC = < DAC.
Because you have parallelogram, <BCA = <DCA as well
If we reflect in the diagonal CA, then the ray AB goes onto ray AC (equal angles)
Also ray CA goes onto ray CD.

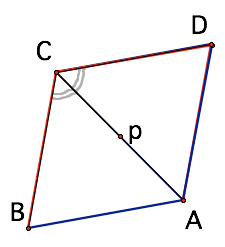
You can then reason why B goes onto D!

This is sufficient to show side BC is equal (in length) to DC - and you are well on the way to completing the proof.

Walter Whiteley

Hi Miguel.

Take a look at the resulting triangles when you create such a diagonal. Can you prove the two triangles are congruent isosceles triangles by looking identifying angles with the same measure?

Stephen.