Hi Ming.

I tried quickly sketching the two graphs y = sin(x) and y = x² - x and I can immediately see two solutions exist:

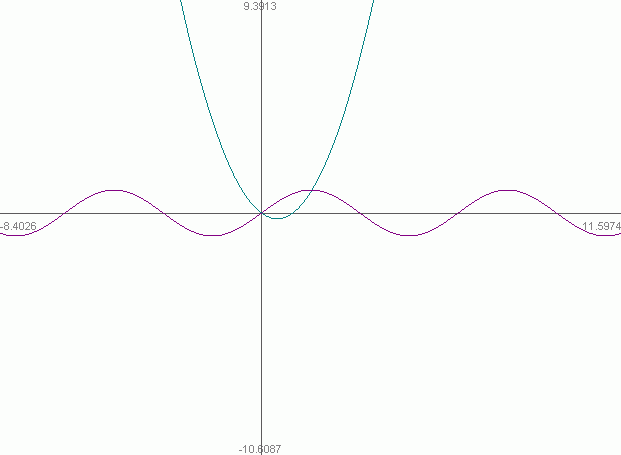
So I use guess-and-check:

x = 0 works because sin(0) = 0² - 0

It looks like y = 1 is close.
However, sin(x) = 1 gives x = pi/2 and 1 = x² - x gives x = phi (the Golden Ratio) and these two values are not the same.

So for the second solution, I can only approximate. To do so, I can use "Newton's Method" to find successively more accurate values of x by starting with an x that is "close" to the solution.

Newton's method says that if you have a function f(x) = 0, then you can start with an x that is close to a root and iterate x_i = x_i-1 - f(x)/f '(x) to get ever more precise.

So f(x) in your case is x² - x - sin(x), which makes f'(x) = 2x - 1 - cosx.

If I start with x = 1.5, then it generates a better approximation for x:

x = 1.5 - [ 1.5² - 1.5 - sin(1.5) ] / [ 2(1.5) - 1 - cos(1.5) ]
x = 1.628284745

Now iterate again:

x = 1.628284745- [ 1.628284745² - 1.628284745- sin(1.628284745) ] / [ 2(1.628284745) - 1 - cos(1.628284745) ]
x = 1.617620013

And again:

x = 1.617620013- [ 1.617620013² - 1.617620013- sin(1.617620013) ] / [ 2(1.617620013) - 1 - cos(1.617620013) ]
x = 1.617545290

And again:

x = 1.617545290- [ 1.617545290² - 1.617545290- sin(1.617545290) ] / [ 2(1.617545290) - 1 - cos(1.617545290) ]
x = 1.617545286

which is such a tiny difference from the previous figure, I decide this is a good enough approximation.

Cheers,
Stephen La Rocque.