| |||
| Math Central | Quandaries & Queries |
|
Question from Muhammad, a teacher: Hi, how can we find the perimeter and area of the region common to two intersecting circles of radii 6 cm and 4 cm with centers 7 cm apart. |
Muhammad,
I can point you at one solution. There may be an easier approach but I don't see it.
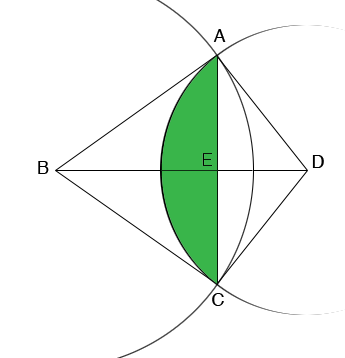
In my diagram the length of BD is 7 cm, the length of BA is 6 cm and the length of DA is 4 cm. Thus you can use the law of cosines on the triangle ABD to find the measure of the angle BDA. Thus you can find the measure of the angle CDA and this the area of the sector CDA.
Looking at triangle AED, it is a right triangle with hypotenuse of length 4 cm and an angle EDA which you know. Thus from Cos(EDA) = |ED|/4 and sin(EDA) = |AE|/4 you can find |ED| and |AE|. Hence you can find the area of triangle AED and if you subtract twice the area of this triangle from the area of the sector CDA you will have the area of the region shaded green in the diagram.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.