Hi Nana.

The closest point on the line AB to the origin is the intersection point X on the line XO that is perpendicular to the line AB. See the diagram below.

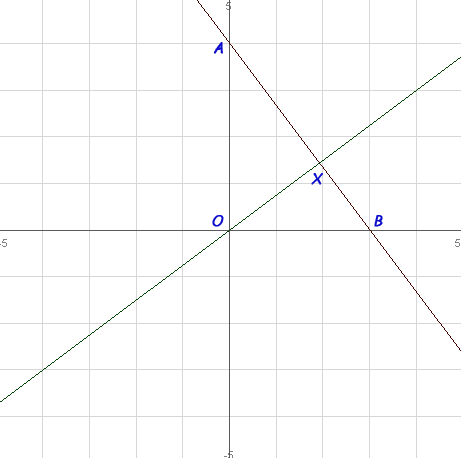
First method:

If you can determine the point of intersection of these two lines (that's point X), you have found the closest point on AB to the origin. Then you can use the distance formula if you want to know the actual distance from X to O.

You will need to know the equation of both lines to find the intersection point. You have the equation of the line AB. The equation of line XO is defined by its slope (the slope of a perpendicular line is the negative reciprocal of the line it is perpendicular to) and a single point (the origin in your case).

Second method:

If you don't care where X is but only want to know the distance XO, then there is an easier way to solve the problem.

The area of a triangle is half the base times the height. So the area of triangle AOB is (1/2)x(3)x(4)=6 square units, using the intercepts described in the question.

However, we could just as accurately choose AB as the base and XO as the height, since these are perpendicular to each other also. Thus, 6 = (1/2) (AB) (XO). Solve this for XO and you have (XO) = 12/(AB). And the length AB is the length of the hypotenuse of right triangle AOB, so you can use Pythagorus to find AB.

Hope this helps,