An isosceles triangle - Math Central

HOME

Math Central

Quandaries & Queries

Question from Nancy, a parent:

I needed to help my 9th grade daughter regarding a geometry problem. After a while I realized I am not getting anywhere. I saw that in 2005 someone asked the same question and you gave them a hint. Unfortunately it still did not help. Because I had figured that much!Can you kindly help me proof this problem?
PX and QY are attitudes of acute triangle PQR, and Z is the midpoint of PQ. Can you write a proof that triangle XYZ is isosceles?
I am sure it is something simple I am missing, but I just can not seem to be able to see it. Thank you much.

Hi Nancy,

Draw the circle through P, Q and X and let C be the centre of the circle. Extend the line segment from P to C to meet the circle at S.

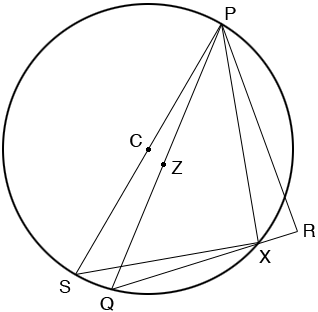
diagram

The angle SXP is subtended by a diagonal and is hence a right angle. But angle QXP is also a right angle and hence Q is on the line joining S and X. Thus S must be Q and hence C = Z.

I hope this helps,
Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.