Water in a paper cup - Math Central

HOME

Math Central

Quandaries & Queries

Question from Nicholas, a student:

Water is leaking out of a small hole at the tip of a conical paper cup at the rate of 1cm^3/min. The cup has height 8cm and radius 6cm, and is initially full up to the top. Find the rate of change of the height of water in the cup when the cup just begins to leak.
Since V= (pi/3)r^2h, how do I eliminate a variable or change the equation so I that I can answer the question? Thanks.

Hi Nicolas,

Draw a diagram of the paper cup when some water has leaked out.

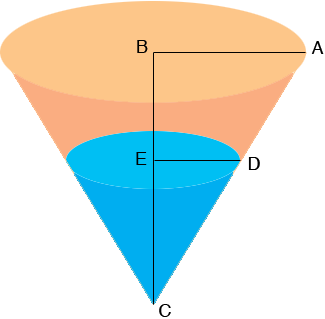
paper cup

Suppose that the height of the water in the cup is |EC| = h and the radius of the surface of the water is |DE| = r. Triangles ABC and DEC are similar so

|AB|/|BC| = |DE|/|EC| so 6/8 = r/h

I hope this helps,
Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.