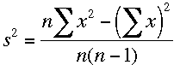| |||
| Math Central | Quandaries & Queries |
|
Question from Nimra, a student: The following sets of data represent the distributions of house prices in the north-east and south-west of a country. Random samples of 100 houses were selected in each region. Number of Number of
(a) Calculate the mean, median and standard deviation for |
Hi Nimra,
I didn't get the complete instructions but I expect they were "Calculate the mean, median and standard deviation for the houses in the NE."
With this grouped data you don't have the exact values so the best you can do is approximate the mean median and standard deviation. I'm going to approximate the mean first.
Look at the first class. There were 5 houses sold foe between 80 and 100 thousand pounds. The middle of the calss is (80 + 100)/2 = 90 thousand pounds. The best estimate of the total value of the 5 houses in this rande is 5 × 90 = 450 thousand pounds.
Look at the second class. There were 9 houses sold foe between 100 and 120 thousand pounds. The middle of the calss is (100 + 120)/2 = 110 thousand pounds. The best estimate of the total value of t9e 5 houses in this rand9 is 11 × 90 = 990 thousand pounds.
Continuing through the classes my best estimate of the total value of the houses sold is
5 × 90 + 9 × 110 + 20 ×130 ··· 4 ×230 thousand pounds. (1)
Since there were 100 houses sold divide this total by 100 to approximate the mean house price of the houses sold.
For the standard deviation calculatiion I would use the expression of the variance which is
The sum of the x values is approximated by expression (1) above. To approximate the sum of the squares of the x values use the same logic. The first 5 x values are approximately 90 so the sum of their squares is approximately 5 × 902 etc. so the sum of the squares of the x values is approximately
5 × 902 + 9 × 1102 + 20 ×1302 ··· 4 ×2302 (thousand pounds)2.
The median is between the 50th and 51st values. You might just say that the median is between 140 and 160 thousand pounds. You might approximate it my the middle of this class, 150 thousand pounds. You might also do the following. There are 5 + 9 + 20 = 34 values before the class containing the median. This class is 160 - 140 = 20 units long and you need to go 50.5 - 34 = 16.5 units to arrive at the median value. Thus another approximation of the median is
140 + 16.5/35 × 20 = 149.4 thousand pounds.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.