| |||
| Math Central | Quandaries & Queries |
|
Question from paula, a teacher: Application: The Grain Silo Problem Farmer John stores grain in a large silo located at the edge of his farm. The cylinder-shaped silo has one flat, rectangular face that rests against the side of his barn. The height of the silo is 30 feet and the face resting against the barn is 10 feet wide. If the barn is approximately 5 feet from the center of the silo, determine the capacity of Farmer John's silo in cubic feet of grain. Hint: Look for connections between this problem and the problem you solved in Part 1 of this week's Discussion (a square inscribed in a circle). Describe how you solved this problem and include your solution. How did working through this problem help you further develop your understanding of capacity and volume as it relates to cylinder-type shapes? |
Hi Paula,
I can help you get started. I drew a cross-section of the silo.
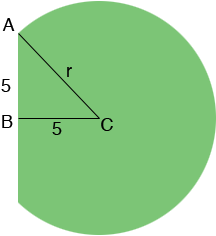
B is the midpoint of the face that rests against the side of the barn and hence the length of AB is 5 feet.
I see two facts that come from the diagram. Since the |AB| = |BC| the angle BCA has measure 45o. Since triangle ABC is a right triangle you can use Pythagoras theorem to find the length |CA| which is the radius r of the circular base of the silo.
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.