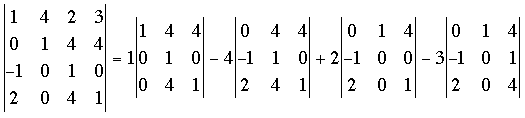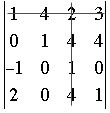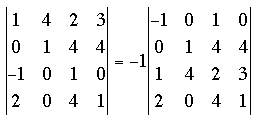Rav,

A 4 by 4 determinant can be expanded in terms of 3 by 3 determinants called minors. Let's look at an example

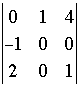
Here I have expressed the 4 by 4 determinant in terms of 4, 3 by 3 determinants. To see what I did look at the first row of the 4 by 4 determinant. This row is 1, 4, 2, 3. These are the coefficients of the 3 by 3 determinants but with alternating signs, that is 1, -4, 2, -3. Each of these coefficients is multiplied by the 3 by 3 determinant obtained by removing the row and column of the 4 by 4 determinant that contains this coefficient. For example looking at the 2 in the first row of the 4 by 4 determinant, the minor obtained by removing the first row and third column is

or

Many possible simplifications of this calculation can be made using properties of determinants. I am going to mention just one.

If you interchange two rows of a determinant then the value of the new determinant is -1 times the value of the old determinant. Thus is our example of you interchange the first and third rows you obtain

Now if you expand this new determinant across the first row using minors two of the resulting 3 by 3 determinants have a coefficient of 0 hence simplifying the calculation.

There is much more to say about the evaluation of determinants of any dimension. For example I suggest you look at the properties of determinants on MathWorld. They appear between equations 28 and 29 on this page.

Harley