| |||
| Math Central | Quandaries & Queries |
|
Question from Rita, a student: A surveillance satellite circles Earth at a height of h miles above the surface. Suppose that d is the distance, in miles, on the surface of Earth that can be observed from the satellite. (a) Find an equation that relates the central angle theta to the height h. (b) Find an equation that relates the observable distance d and theta. (c) Find an equation that relates d and h. NOTE: radius of Earth is given to be 3960 miles |
Hi Rita,
I can get you started.
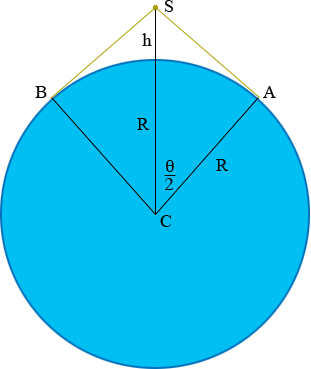
S is the satellite, C is the centre of the Earth, R is the radius of the Earth (3960 miles) and the length of the arc BA is d. The measure of angle NCA is θ and hence by the symmetry the measure of the angle SCA is θ/2.
Since the line segment SA is tangent to the surface of the Earth, angle SAC is a right angle. Thus the side CA of triangle SCA is adjacent to angle SCA and SC is the hypotenuse of the triangle. What trig function relates the adjacent side and the hypotenuse to the angle? This give an answer to part a).
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.