| |||
| Math Central | Quandaries & Queries |
|
Question from Rita, a student: A space camera circles the Earth at a height of h miles above the surface. Suppose that d distance, IN MILES, on the surface of the Earth can be seen from the camera. (a) Find an equation that relates the central angle theta to the height h. (b) Find an equation that relates the observable distance d and theta. (c) Find an equation that relates d and h. (d) If d is to be 3500 miles, how high must the camera orbit above Earth? (e) If the camera orbits at a height of 400 miles, what distance d on the surface can be seen? |
Hi Rita,
If you draw a diagram you realize that the line of sight from the camera to the horizon is tangent to the surface of the earth and hence in the diagram below the angle CAB is a right angle.
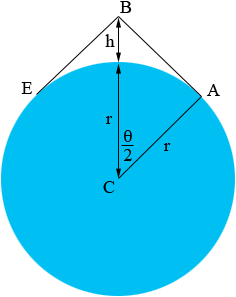
What trig function relates r, r + h and the angle BCA? This gives you an equation that relates h and theta.
The observable distance d is the length of the arc from E to A. What is the equation that relates the arc length, the radius r and the angle theta?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.