Hi,

Fix two vertices A and B to form one side of a triangle. Now choose another point C not on the line joining A and B and construct the triangle ABC. I can then construct a triangle ABD with a smaller perimeter than your triangle by placing D half way between A and C.

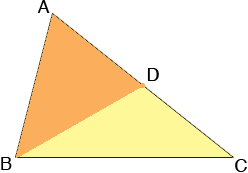
The point here is that no matter what triangle you choose with side AB I can always construct a triangle with side AB that has a smaller perimeter than yours. Thus it's not possible to choose a third point that results in the smallest possible perimeter.

Penny

RS wrote back

Thanks very much. Perhaps I did not make phrase my question correctly. With two points fixed and the third point variable but along a straight line, then which is the smallest triangle. Please see attached diagram.

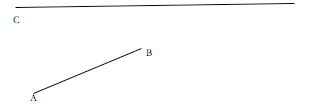
Regards

RS

Hi,

You drew the line as if it is horizontal but I don't want to make that assumption. Here is my diagram. I called the line L.

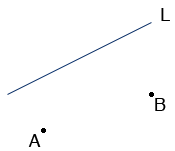
Reflect the point B in the line L to obtain a new point B'. Join A and B'. Let K be the point where this line meets L.

Claim: The triangle ABK has the least perimeter of any triangle ABX where X is on L.

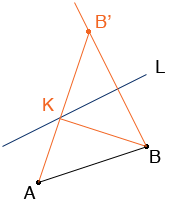
Since |KB| = |KB'| the perimeter of ABK is |AB| + |AB'|. If X is any other point on L then |XB| = |XB'| and the perimeter of ABX is |AB| + |AX| + |XB'|.

But |AX| + |XB'| > |AB'|.

We are not sure what you are trying to do but if you are trying to construct the point K here is one procedure.

Put a coordinate system on the plane. Let A = (a₁, a₂), B = (b₁, b₂) and L be the line y = mx + b.

1. Subtract b from all the y-coordinates. This moves the line to y = mx which passes through the origin.
   
   
2. Rotate the diagram so that the line L lies along the x-axis. The angle between the x-axis and L is tan(m) so rotate through an angle of - arctan(m). This rotation can be accomplished by multiplication by the matrix 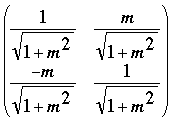Let NA and NB be the new positions of A and B after subtracting b from the y-components and rotation by the matrix.
   
   
3. Let NB have coordinates (nb₁, nb₂). Reflect NB through the x-axis to the point NB' (nb₁, -nb₂).
   
   
4. Rotate the point NB' through the angle arctan(m). This can be accomplished by multiplication by the matrix 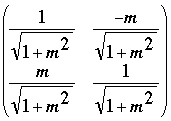Finally add b to the y-coordinate of the rotated point and the resulting point is B'.
   
   All that remains is to write the equation of the line through A and B' and find its intersection K with the line L.

Chris and Penny