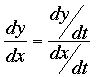| |||
| Math Central | Quandaries & Queries |
|
Question from Russell, a student: A particle moves in the xy-plane with X = 2t^3 - 12t^2 + 18t Y = 3t^4 - 28t^3 + 72t^2 find an equation of the line tangent to the given curve at t_0_ = 1 note: t_0_ is t subscript 0
|
Hi Russell,
To find the equation of the tangent line you need the x and y coordinates of a point on the line and its slope. The point is described by t0 = 1 and hence you can find the x and y coordinates by substituting t = 1 into the equations for x and y.
The slope of the tangent line at the point is dy/dx at that point. You can find dy/dx using
Thus find dy/dt and dx/dt. Form dy/dx and simplify. Substitute t = 1 to find the slope of the tangent at the point.
Now that you have the x and y coordinates of a point on the line and its slope write its equation.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.