| |||
| Math Central | Quandaries & Queries |
|
The diagram shows the curve y=(2x-5)4. The point P has co-ordinates (4,81) and the tangent to the curve at P meets the x-axis at Q. Find the area of the region (shaded in the diagram) enclosed between the curve, PQ and the x-axis . (Please note that the equation y is read as y=2x -5 whole raise to power 4.) Regards, Sabahat |
Sabahat,
Here is the diagram you sent
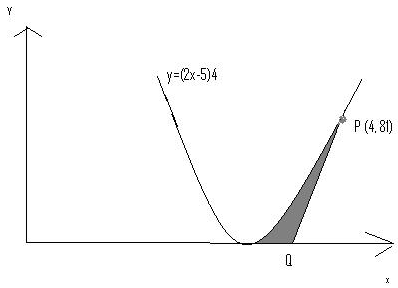
Take the derivative of the curve in order to evaluate the slope of the tangent line. Calculate the area under the tangent line and above the x-axis (it is a triangle, so this is the easiest step). Also use this to find the x value of point Q.
Now take the definite integral of the curve evaluated between 2.5 and the x value of P. The value 2.5 is the zero for the function (you can see it by inspection or prove it).
Finally subtract the triangular area from the definite integral value to find the area of the shaded region.
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.