Sabahat,

I changed the problem slightly by changing the curve to y = 1/2 x³ + 1. The region enclosed by the two axes x = 2 and the curve is shaded ping in the diagram below.

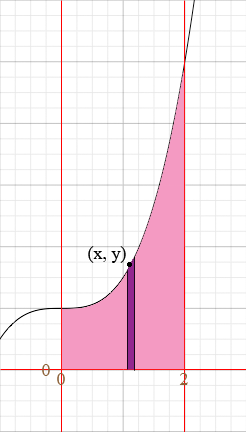
I am going to use cylindrical shells to calculate the volume so I took a strip of thickness Δx (shaded purple) and a point (x, y) on the curve at the top of the strip. This strip is then revolved around the y-axis to form the cylindrical shell in the diagram on the left below. This shell is then sliced from bottom to top and rolled out flat to form what is approximately the rectangular slab on the right in the diagram below.

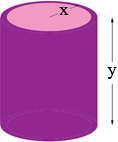Since the radius of the shell is approximately x, the length of the slab is approximately the circumference of a circle with radius x which is 2 π x. Thus the volume of the slab is approximately

2 π x y Δx.

Since (x, y) is on the curve y = 1/2 x³ + 1 and hence the volume of the slab is approximately

2 π x (1/2 x³ + 1) Δx.

To approximate the volume you want, subdivide the interval from 0 to 2 into pieces of length Δx, form the strips as in the first diagram, revolve each strip around the y-axis and add the volumes of the resulting cylindrical shells. Now take a limit as the thickness Δx of the strips approaches zero and the sum of the volumes of the cylindrical shells approaches the integral of

2 π x (1/2 x³ + 1) dx = π (x⁴ + 2x) dx

from x = 0 to x = 2.

I hope this helps,
Harley