| |||
| Math Central | Quandaries & Queries |
|
Question from Sabrina, a student: A railroad bridge is 20m above, and at right angles to, a river. A person in a train travelling at 60 km/h passes over the centre of the bridge at the same instant that a person in a motorboat travelling at 20km/h passes under the centre of the bridge. How fast are the two people separating 10s later? |
Hi Sabrina,
You have distance measured in metres and kilometres and time in hours and seconds. We need to decide on consistent units so I am going to measure distance in metres and time in seconds. There are 1,000 metres in a kilometre so 60 km/h is 60,000 m/h. There are 60 minutes in an hour and 60 seconds in a minute so there are 60 × 60 = 3,600 seconds on an hour. Thus 60,000 m/h is 60,000/3,600 m/s which simplifies to 100/6 m/s. Hence the train is travelling at 100/6 m/s. You can find the speed of the boat in metres per second.
In my diagram P is the position of the train and Q the position of the boat when the train is directly over the boat. T is the position of the train and B the position of the boat t seconds later.
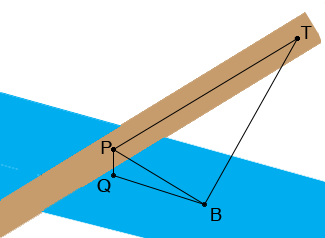
The distance from P to Q is 20 metres. Since you know the speed of the train and the boat you can find the distance from P to T and the distance from Q to B, both of these are functions of time..
Triangle PQB is a right triangle so you can use Pythagoras theorem to find the distance from P to B. Triangle TPB is also a right triangle so you can again use use Pythagoras theorem to find the distance from T to B. I am going to call this distance f(t). Your problem is to find f '(10).
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.