Hi Scott.

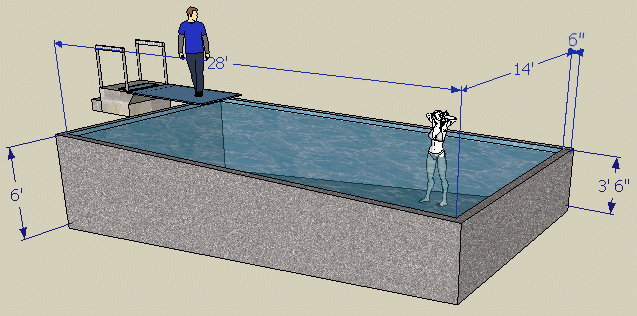
I will have to assume the bottom is just a constant slope from one side to the other for this. I also assume the dimensions you provided are the size of the shape that the water fills, around which the concrete will be formed.

The easiest way to calculate the amount of concrete you will need is to subtract the hollow inside volume from the concrete exterior.

The volume of a shape like yours can be calculated by multiply the area of the side of the pool by its width.

The side of your pool is a trapezoid. The area of a trapezoid is the average of the parallel sides times the distance they are apart from each other.

So the concrete box's side area is (4 + 6.5)/2 x 29 feet. That equals 152.25 square feet. Its width is 15 feet, so 152.25 x 15 = 2284 cubic feet.

Likewise, the inside (water space) of the pool is (3.5 + 6)/2 x 28 feet by a width of 14 feet. That makes 1862 cubic feet.

Subtracting these gives us the volume of concrete: 2284 - 1862 = 422 cubic feet.

To convert that to cubic yards for the concrete supplier, you'd divide by 27 (because 3 feet = 1 yard and since you are dealing with cubic feet, 3³ feet³ = 1³ yard³).

422/27 = 15.6 cubic yards of concrete.

Hope this helps,
Stephen La Rocque.