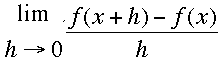Differentiate x^(1/3) using first principles

HOME

Math Central

Quandaries & Queries

Question from Sheila, a student:

hi!
our teacher gave us this question as a challenge and even he couldn't figure it out:
Differentiate x^(1/3) [aka the cube root of x] using first principles. i know the answer is 1/(3.x^2/3), but how is it possible using first principles?
thank you,
Sheila

Hi Sheila,

If f(x) = x^1/3 then you need to evaluate

and the numerator is

(x + h)^1/3 - x^1/3

Let a = (x + h)^1/3 and b = x^1/3 and recall the difference of cubes

a³ - b³ = (a - b)(a² + ab + b²)

Multiply the numerator and denominator inside the limit by (a² + ab + b²) and the numerator becomes

a³ - b³ = (x + h) - x = h

and the denominator becomes

h[(x+h)^2/3 + x^1/3 (x + h)^1/3 + x^2/3]

The numerator and denominator each have a factor of h which will cancel and then you can take the limit as h approaches zero.

I hope this helps,
Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.