Hi Sheldon,

An octagon is an eight sided polygon and it can have any shape. Maybe

or even

I expect however that you want one that has horizontal and vertical symmetry like

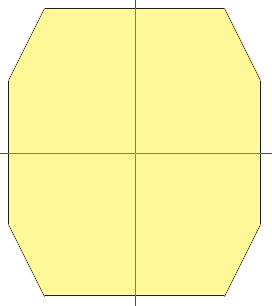
Here the red lines are lines of symmetry.

If so you still have some choices to make. Suppose you decide that the top and bottom are each 2x inches long and the right and left sides are each 2y inches high.

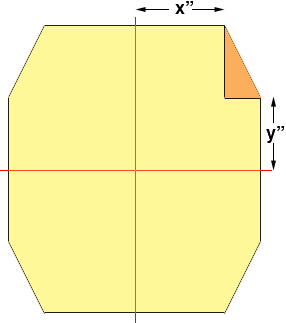
Now focus on the triangle i the upper right corner. Since the width of the octagon is 16 inches the base PQ of the triangle is 8 - x inches long and since the height of the octagon is 20 inches the height RP of the triangle is 10 - y inches.

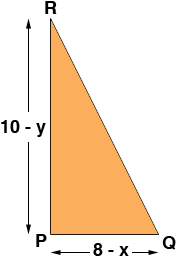
Thus Pythagoras' theorem tells us that

|QR|² = (8 - x)² + (10 - y)²

Thus if you specify the lengths of the top, bottom and two vertical sides of the octagon, calculate |QR|² using the expression above and then take its square root you will have the lengths of the four remaining sides.

I hope this helps,
Penny