Hi Shubha.

Hopefully I am thinking of the easiest way to solve the problem, but start by drawing the following diagram:

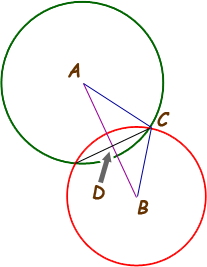
You can see the scalene triangle ABC in this diagram. If we let d = the distance |AB| and h = the distance |CD|, then the question is asking for the value of 2h. Let's now redraw this without the circles:

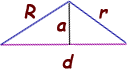
You should recognize that the chord and the radial line AB are perpendicular, so a is the height of triangle ABC and d is its base.

You can re-arrange each of the circle equations into standard circle form which allows you to read off the radius and the center position of each circle. Assign one radius as R and the other as r.

Use the distance formula to calculate the distance between the two centers (that's d). So now you have numbers for all the sides of the triangle except the height a.

The height of a triangle times half its base is the area of the triangle. As well, any scalene triangle with known side lengths has an area that can be calculated using Heron's Formula. So calculate the area using Heron's formula and use that together with the distance d as the base to find the height a.

Cheers,
Stephen La Rocque.