Hi Simon.

Maybe this diagram will help you visualize it. Mine is an Aussie skateboarder under a streetlight though.

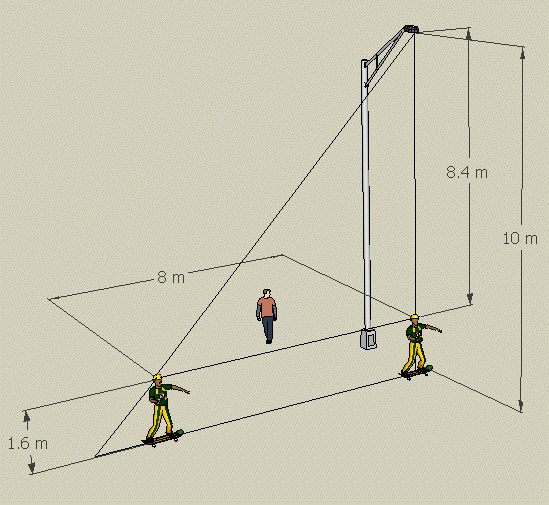
After one second, the skater has gone 6 meters. But the shadow tip has obviously gone farther, right?

These are similar triangles, so you can find the length of the shadow if you like.

The important thing is the relationship between the shadow's length and the skater's position.

The skater's speed is 6 m/s, so her distance from the starting position is 6t where t is the time in seconds. Thus in the right triangle above the skater's head the ratio of the base to the height is (6t / 8.4).

Look now at the biggest triangle. Let S be the length of the base of this triangle in metres. This triangle is similar to the triangle in the paragraph above and the ratio of its base to its height is S / 10. Since the triangles are similar

6t/8.4 = S/10 so S = (60/8.4) t

Thus the speed at which the shadow's head is moving is the derivative of this with respect to time. This may seem counterintuitive as the speed is constant and doesn't depend on the distance from the skater to the starting point.

Stephen and Harley