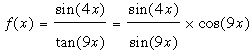| |||
| Math Central | Quandaries & Queries |
|
Question from stev, a student: as x->0. How do you find the limit of f(x)=(sin4x)/(tan9X) Thank you |
Hi Stev,
First write tan(9x) as sin(9x)/cos(9x) and f(x) can then be written
As x approaches 0, cos(9x) approaches 1. Thus all that remains is to find the limit of sin(4x)/six(9x) as x approaches zero. For this I suggest you look at the responses Stepehen and I gave to Josh for his problem.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.