We have two responses for you

Hi Steven,

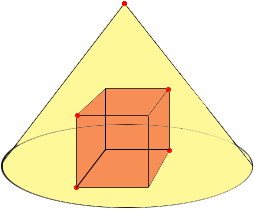
Since the cube is inscribed in the cone the vertices on the top face of the cube lie on the cone. Slice the diagram by a vertical plane that passes through the 5 red points. Her is the resulting plane diagram where x is the length of a side of the cube.

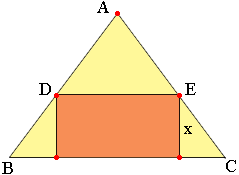
Can you see how to use this diagram to find x?

Harley

Steven,

I'm going to assume that the base of the cube coincides with the base of the cone.

Can you figure out the side length of the largest square that can be inscribed in an isosceles triangle with base 4 and height 5? After that, you can use the properties of the cone to argue that this is the side length of the largest cube that can be inscribed in the cone.

Good luck,
Victoria