A sector of a circle - Math Central

Math Central

Quandaries & Queries

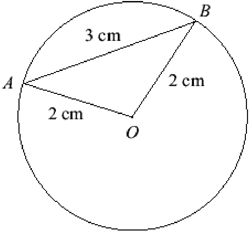
hi im stuck on this question. i have tried to do some, could you please check it and help me.
the answers i have worked out are in red.
the question is attached. thank you.

In this question you should give your answers correct to three decimal
places.

(a) The circle below has radius 2 cm, and the chord AB has length 3 cm.
O is the centre of the circle.

circle

Show that AOB is 1.696 radians (to three decimal places).

Angle(AOB) = π - 2θ ≈ π - 1.446 ≈ 1.696 radians.

Hence find the area of the (smaller) sector AOB.
Find the area of the triangle AOB.

draw a line from the origin to the midpoint of AB.

This splits the triangle into two right triangles, each with
hypotenuse 2, and adjacent side = 1.5

cos θ = adjacent / hypotenuse = (1.5) / 2 = 0.75

θ = arccos (0.75) ≈ 0.723 radians

Area of one of the small right triangles is (1/2)bh

Need to find h (length of segment from 0 to midpt AB)

sin θ = opposite / hypotenuse

opposite = (hypotenuse) * sin θ = 2 * sin (0.723 radians)
≈ 1.323 cm

So area of one of the small right triangles
≈ (1/2) (1.5) (1.323) ≈ 0.992 cm^2

Area of triangle AOB is two times this amount or ≈ 1.984 cm^2

Hence find the (smaller) area enclosed between the chord AB and the circle.
Express both the area of the sector and the area from part (a) (4) as percentages of the area of the circle.

Hi,

I don't see where you obtained θ in part 1. I would have used the law of cosines to determine the angle AOB.

In part 2. the area of a sector with central angle θ expressed in radians is 1/2 r² θ and you know θ from part 1.

I agree with your answer in part 3.

The answer to part 4. is the difference between the area of the sector (part 2.) and the area of the triangle (part 3.).

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.