| |||
| Math Central | Quandaries & Queries |
|
Question from sunday, a student: I'm doing a unit assessment, and there is something I don't understand. Now in my textbook, it says that surface area for a cube is different from a cylinder. Surface area for a cylinder has two numbers, but surface area for a cube has 3 or more numbers. And plus, I can't figure out the volume for a cube because it only shows volume for a cylinder. So how do I get this right? |
Hi,
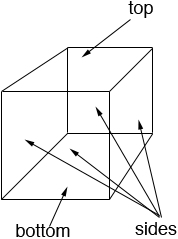
Imagine that you want to construct a cube out of paper. You need to cut 6 identical (congruent) pieces, 1 for the bottom, one for the top and 4 for the sides. Each of these 6 pieces is a square.
For a cube each of the three dimensions length, width and height are the same. I'm going to call this measurement L units.
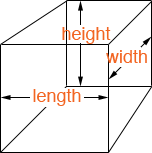
Thus each of the 6 congruent squares you need to construct the cube is L units by L units and hence has area L × L = L2 square units.
Hence the total surface area of the cube is 6 × L2 square unit
How do you find the surface area of a cylinder, like a soup can? Suppose the radius of the top of the can is r and the height of the can is h. First use a can opener and cut off both the top and bottom of the can.
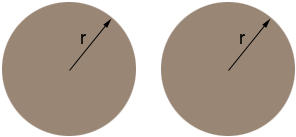
The can is then in three pieces, two of which are congruent circular disks with radius r. The area of a circular disk of radius r is π r2 and thus the area of the two disks is 2 π r2. The third piece is a cylindrical shell, h units high and the distance around is the length of the circumference of a circle of radius r which is 2 πr.
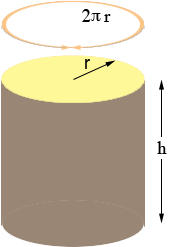
Slice this piece of the can from bottom to top and roll it out flat. It forms a rectangle 2 πr units long and h units high.

The area of a rectangle is the length times the width so the area of this rectangle is
2 π r h.
Thus the surface area of a cylinder is
2 π r2 + 2 π r h.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.