| |||
| Math Central | Quandaries & Queries |
|
Question from svetik, a student: On Thanksgiving Day, a group of nutty professors dressed up as "turkeys" and participated in a local fundraising event. The event consisted of three types of races: the sprint, the relay, and the hurdles. One more "turkey" takes part in the hurdles only than the sprint only. The same number take part in the sprint and the hurdles as take part in the relay and the hurdles. Eleven of the "turkeys" taking some part in these three races do not do the relay. Five "turkeys" take part in the sprint and the relay and three enter all three races. There are four teams of four "turkeys" in the relay. And, one more "turkey" is running in both the relay and the sprint than in the hurdles only. "Turkey" Coe turned and said to "Turkey" Kim, "How many 'turkeys' were taking some part in any of the three races?" The nuttiest math professor, "Turkey" Young, said "There were _______ 'turkeys' taking part in any of the three races."
Fill in the blank!!! |
Svetik,
I can help you get started. I drew three overlapping circles to represent Sprint, Relay and Hurdles. This partitions the turkeys into 7 distinct, non-overlapping groups and I represented the number of turkeys in each group by a letter from a to g. What you are looking for is a + b + c + d + e + f + g.
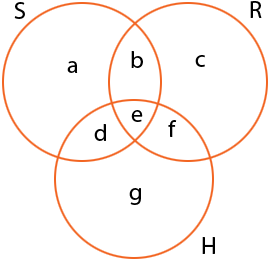
Now read the clues and see what they they tell you about a to g, keeping in mind that you want the sum of a to g. I'll do one
One more "turkey" takes part in the hurdles only than the sprint only.
The number of turkeys that take part in the sprint only is a.
The number of turkeys that take part in the hurdles only is g. Thusg = a + 1.
Have fun with this,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.