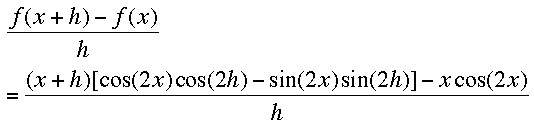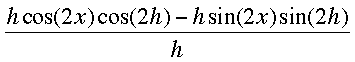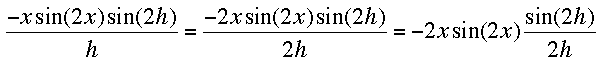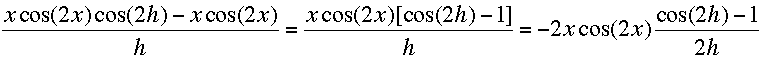Taiwo,

The first thing to notice when you see y = x cos(2x) is that it is a product of two functions, y = x and y = cos(2x). Hence you need to apply the product rule. Thus

d/dx[x cos(2x)] = d/dx[x] cos(2x) + x d/dx[cos(2x)] = cos(2x) + x d/dx[cos(2x)]

What remains id to differentiate cos(2x). This involves use of the chain rule.

d/dx[cos(2x)] = -sin(2x) d/dx[2x] = -sin(2x) × 2 = -2 sin(2x)

Hence I get

d/dx[x cos(2x)] = cos(2x) -2x sin(2x)

Penny

Taiwo wrote back

to penny,

dear penny, thanks for the solution. i got the same answer but i was thinking maybe i was wrong. is that a first principle rule method of solving the problem y=xcos2x?. thank you

Taiwo,

If you are going to solve this from first principles you need to know

lim[(sinx)/x] = 1 as x approaches 0
lim[(1 - cosx)/x] = 0 as x approaches 0 and
cos(x + y) = cos(x) cos(y) - sin(x) sin(y)

From first principles you want to evaluate the limit of [f(x + h) - f(x)]/h as h approaches 0 where f(x) = x cos(2x). Evaluating this expression and using the multiple angle expression for the cosine above I got

I then multiplied through by (x + h) and collected terms to express the fraction above as the sum of three fractions

Taking the limit of each of these fractions as h approaches zero I get

1. cos(2x)
   
   
2. -2x sin(2x)
   
   
3. 0

which agrees with the answer you and I both got using the product rule and the chain rule.

Penny