We have two responses for you

Hi Tom,

The x-intercepts are the x-coordinates of the points where the graph crosses the x-axis. In other words they are the x-values of the points (x, 0) on the graph, or the values of x so that f(x) = 0. The task then is to solve f(x) = 0 for x.

f(x) = 0
5sin(4x + π/4) = 0
sin(4x + π/4) = 0

If you look at the graph of y = sin(t) you can see that is crosses the t-axis at t = nπ where n is an integer, positive or negative.

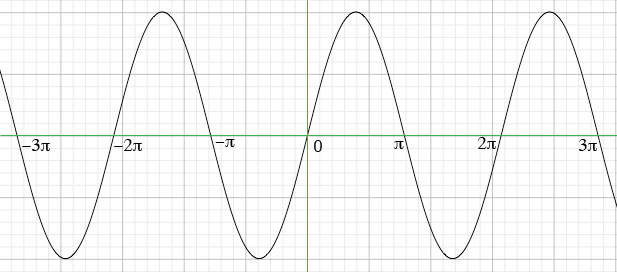
y = sin(t)

Thus the solutions of sin(4x + π/4) = 0 are 4x + π/4 = nπ where n is an integer.

You solved this for the case when n = 0. Solve 4x + π/4 = nπ for x to find all the x-intercepts.

Harley

Hi Tom,

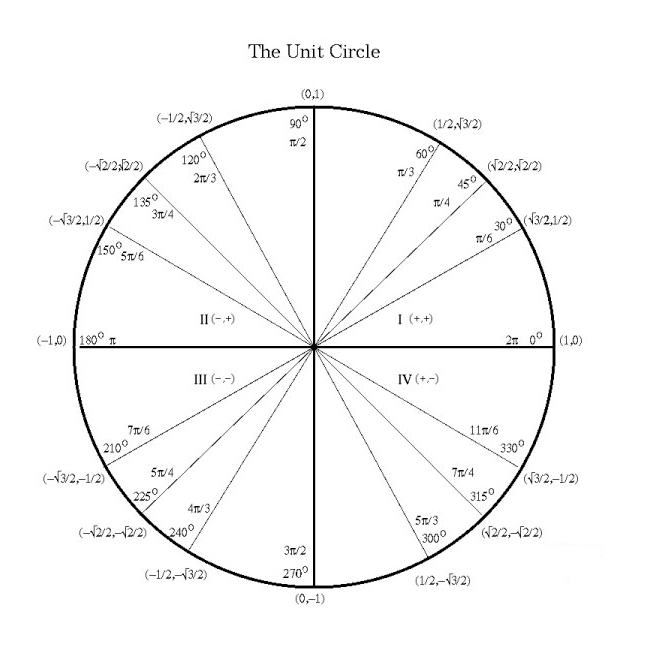
The answer you found is in radians which is a measure of angles, just like degrees. In radians, 180 degrees = pi. If you think of a circle with radius of 1 (which is called the unit circle), you can see the circle below is divided up into some common angle written in degrees and radians.

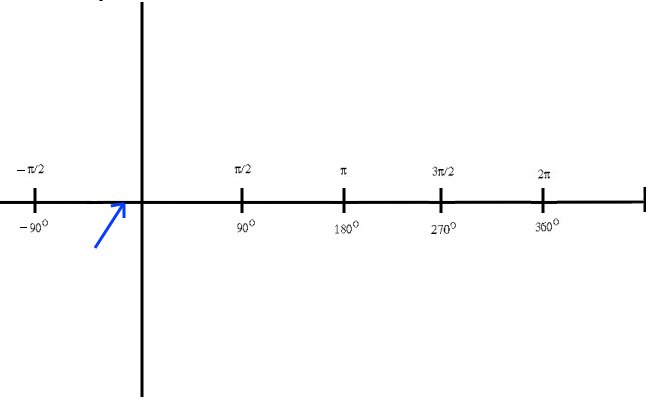
If you take that circle and stretch out into a straight line over the x axis, you can see that the x - intercept you found is slightly to the left of the y axis. Don't forget that since sine is a periodic function, it will have more than one x-intercept.

Janice