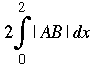Hi Tom,

I think the intent of the problem is to say there is a fixed diameter of the circular base and any cross section perpendicular to the base and perpendicular to this diameter is an isosceles triangle with height 1. Imagine that you slice this solid with a knife that is perpendicular to the base and perpendicular to this diameter like you were slicing a loaf of bread.

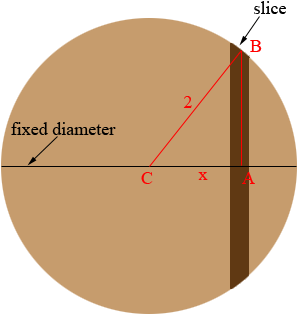
Base

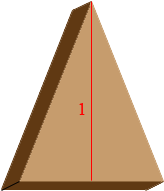
Slice

The face of the slice is an isosceles triangle with height and the volume of the slice is approximately the area of the triangle times the thickness. Half the base of the triangle is the distance AB in the base diagram so the volume of the slice is approximately

|AB| × thickness.

integration theory then tell you that the volume of the solid (the entire loaf) is

Triangle ABC is a right triangle so you can use Pythagoras theorem to find |AB|. Then evaluate the integral to find the area.

If you need further assistance write back,
Harley